
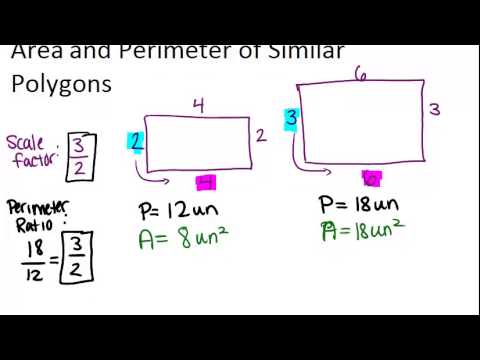
We divide by 2 when we wish to find the actual measurement.\( \newcommand\): Powers of the Golden Ratioįind the following using the golden power rule: a. Depicting something in the scale of 2:1 all measurements then become twice as large as in reality. If you already have these two measurements just insert them into the calculator above and aspect ratio will be calculated as a result. The same mathematics applies when we wish to enlarge. In order to find out the aspect ratio of an image or video, both width and height should be known in advance. In a scale model of 1:X where X is a constant, all measurements become 1/X - of the real measurement. So we can match 6.4 with 8, and so the ratio of sides in triangle S to triangle R is: Now we know that the lengths of sides in triangle S are all 6.4/8 times the lengths of sides in triangle R. For instance, a ratio of 1 pencil to 3 pens would imply that there are three times as many. If we wish to calculate the inverse, where we have a 20ft high wall and wish to reproduce it in the scale of 1:4, we simply calculate: The 6.4 faces the angle marked with two arcs as does the side of length 8 in triangle R. Thus any measurement we see in the model would be 1/4 of the real measurement. For example, the scale of 1:4 represents a fourth. (not the same side length) - that kind of relationship is called triangle similarity.
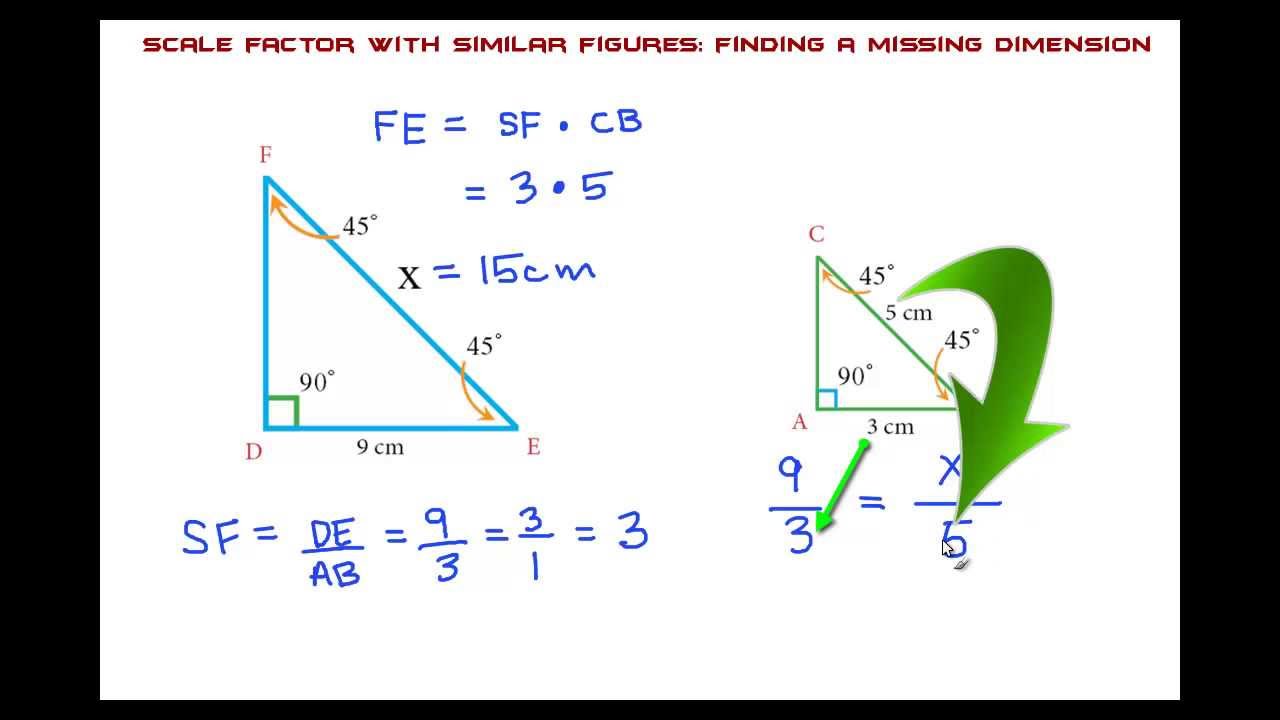
Therefore, you can find the missing terms using nothing else than our ratio calculator Trigonometry has plenty of applications: from. One may scale up (enlarge) or scale down (reduce). Our trigonometry calculator can support you in finding. Scaling involves recreating a model of the object and sharing its proportions, but where the size differs. We often use scaling in order to depict various objects. If the vectors point in opposite directions, the cosine similarity is -1. from diffmatchpatch import diffmatchpatch def computesimilarityanddiff(text1, text2): dmp diffmatchpatch() dmp.DiffTimeout 0.0 diff dmp.diffmain(text1, text2, False) similarity commontext sum(len(txt) for op, txt in diff if op 0) textlength max(len(text1. We already know that if two shapes are similar their corresponding sides are in the same ratio and their corresponding angles are equal. If the vectors point in the exact same direction, the cosine similarity is +1. The builtin SequenceMatcher is very slow on large input, here's how it can be done with diff-match-patch. If you look at a map it always tells you in one of the corners that 1 inch of the map correspond to a much bigger distance in reality. Accordingly, the cosine similarity can take on values between -1 and +1. Thus it equals to zero if there are no intersecting elements and. For instance if one package of cookie mix results in 20 cookies than that would be the same as to say that two packages will result in 40 cookies.Ī proportion is read as "x is to y as z is to w" It uses the ratio of the intersecting set to the union set as the measure of similarity. A ratio is a way to compare two quantities by using division as in miles per hour where we compare miles and hours.Ī ratio can be written in three different ways and all are read as "the ratio of x to y"Ī proportion on the other hand is an equation that says that two ratios are equivalent. Therefore, we know that the similarity ratio is 3:4. For example, if we have the following similarity figure ( ABC EDC), what is the length of a The length of the BC is 3 cm, and the length of the DC is 4 cm. The calculation method is the same as for proportions. Diagram 4 Only the ratio of the BMI Calculator Triangle Calculators. This is called a rate and is a type of ratio. Once you understand the similarity ratio, you can calculate the side lengths. The only thing which varies is their sides. Thats because any scientific calculator (the only ones worth spending. The triangles which are similar have same shape and measure of three angles are also same.

When we talk about the speed of a car or an airplane we measure it in miles per hour. All right triangles with the same leg length ratio will be similar to each other. The Analyzer compares your selected funds annual operating expense ratio to the average for similar funds.


 0 kommentar(er)
0 kommentar(er)
